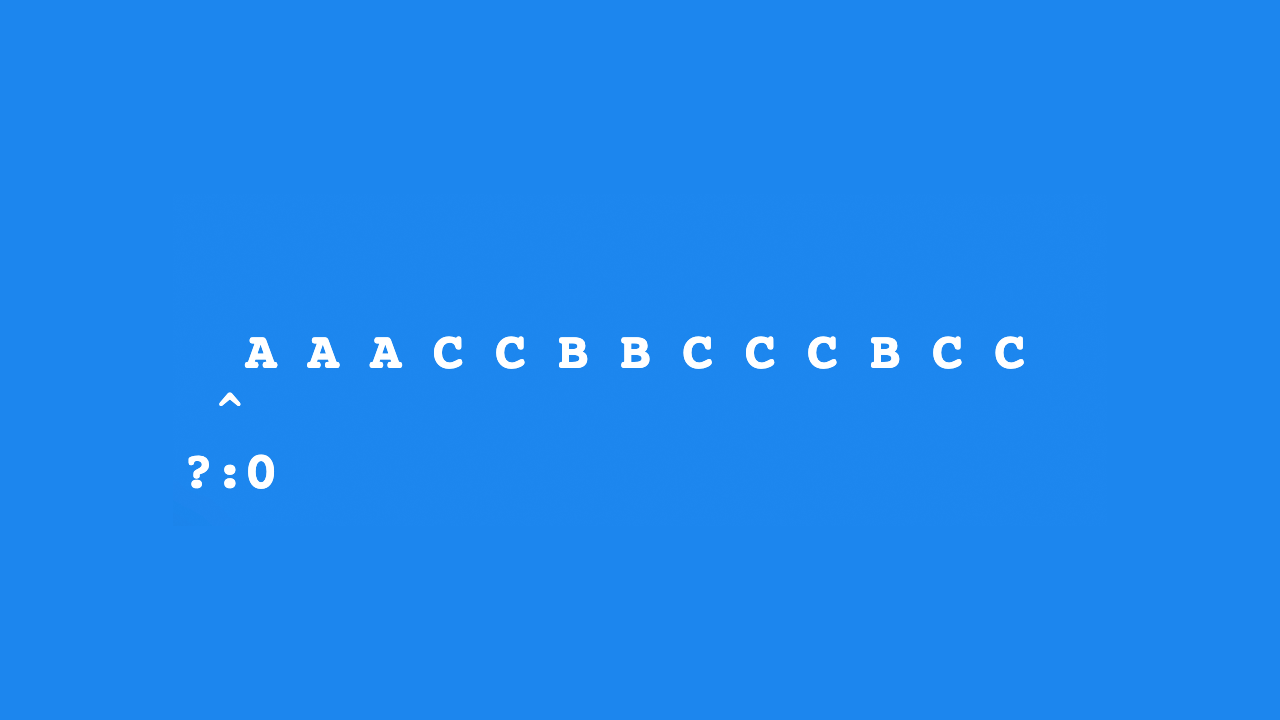Explanation of Boyer-Moore Majority Voting Algorithm

The algorithm

Given a sequence of votes, we want to know who won by majority.

  A A A C C B B C C C B C C
 ^
?:0

We will sweep down the sequence starting at the pointer position shown above.

As we sweep we maintain a pair consisting of a current candidate and a counter. Initially, the current candidate is unknown and the counter is 0.

When we move the pointer forward over an element e:

If the counter is 0 - we set the current candidate to e and we set the counter to 1. If the counter is not 0 - we increment or decrement the counter according to whether e is the current candidate.

When we are done, the current candidate is the majority element, if there is a majority.

How does it work?

For a cadidate to win by majority, they should get more than half of the total votes cast.

A vote counts towards majority of a candidate until there is a vote cast for any of the oppositions.
I.e. a vote is “nullified” in counting toward majority by any other vote that was cast to a different cadidate.

So if someone wants to win by majority, thay would have to have some votes that were not nullified.

Now compare this to this logic to the algorithm written above.

Simulation

Lets say there are 3 cadidates (A B and C) and 13 votes cast.

Initial

  A A A C C B B C C C B C C
 ^
?:0

At first, we don’t know who has majority and how “strong” their majority may be.

Vote 1

A A A C C B B C C C B C C
 ^
A:1

A gets a vote. So we assume A could have majority by the end of counting.

Vote 2

A A A C C B B C C C B C C
   ^
  A:2

A gets aonther vote. It counts towards her majority.

Vote 3

A A A C C B B C C C B C C
     ^
    A:3

A gets aonther vote. It counts towards her majority.

Vote 4

A A A C C B B C C C B C C
       ^
      A:2

C gets a vote. A‘s majority is hurt. But this vote doesn’t count towards C‘s majority. It only “hurts” A.

Vote 5

A A A C C B B C C C B C C
         ^
        A:1

C gets another vote. A‘s majority takes more damage.

Vote 6

A A A C C B B C C C B C C
           ^
          ?:0

B gets a vote now. A‘s majority is hurt even more. Inface, no one has majority at this moment.

Vote 7

A A A C C B B C C C B C C
             ^
            B:1

B gets another vote. It counts towards B‘s majority.

Vote 8

A A A C C B B C C C B C C
               ^
              ?:0

C gets a vote. B‘s majority is hurt.

Vote 9

A A A C C B B C C C B C C
                 ^
                C:1

C gets a vote. At last C has a vote that counts towards C‘s majority. All the other votes were used to counter-balance oppositions.

Vote 10

A A A C C B B C C C B C C
                   ^
                  C:2

C gets another vote. It counts towards C‘s majority.

Vote 11

A A A C C B B C C C B C C
                     ^
                    C:1

B gets a vote. C‘s majority is hurt.

Vote 12

A A A C C B B C C C B C C
                       ^
                      C:2

C gets another vote. It counts towards C‘s majority.

Vote 13

A A A C C B B C C C B C C 
                         ^
                        C:3

C gets another vote. It counts towards C‘s majority.

C is the winner!

Hope this simulation helps someone.

Example was taken from Moore’s website.